What are Option Greeks?

Introduction: Option prices are determined by a number of factors that influence the position’s potential risk and reward. These factors, often referred to as the “Greeks”, are the quantities representing the sensitivity of the price of the option to a change in the underlying parameter, such as price movement, time, risk-free interest rate, or volatility. A few of the most commonly-referenced Greeks include:
 

First-order Greeks

Delta

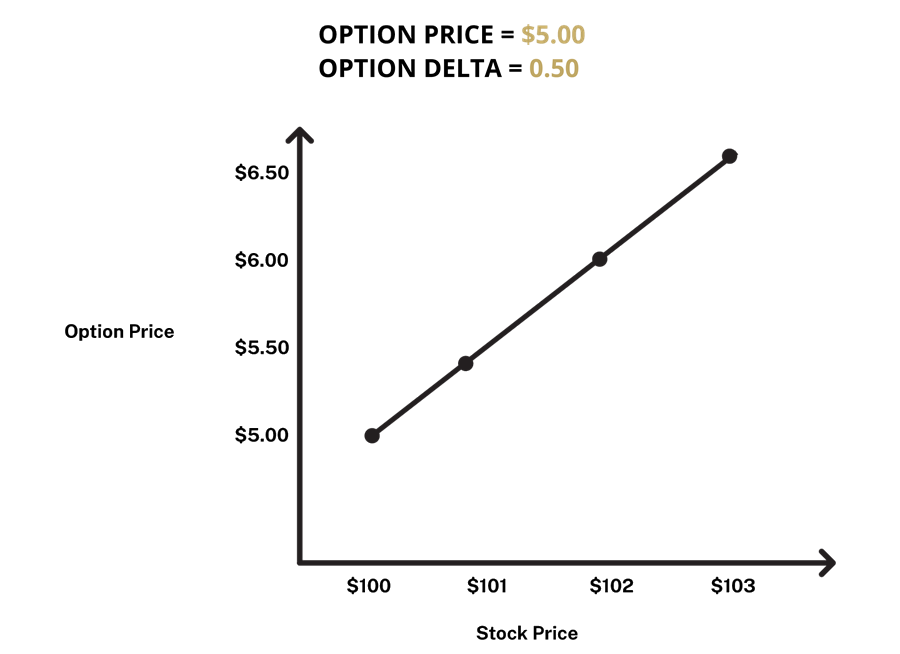
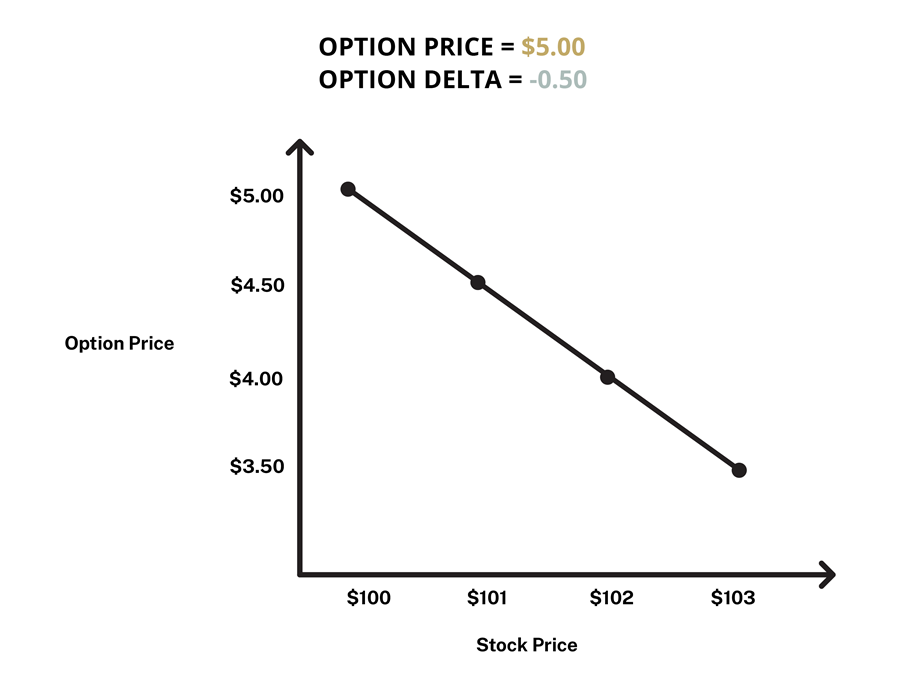
Delta measures the sensitivity of the price of the option contract relative to every $1 move in the underlying investment’s price. Delta readings are measured in decimals between 0 and 1 for call options and 0 and -1 for put options.

Example #1 (Figure 1): If you purchased an at-the-money $100 strike AAPL call option contract for $5.00 with a delta of 0.5 and the price of AAPL increases to $101, all else equal, the price of the contract would increase to $5.50.

Example #2 (Figure 2): If you purchased an at-the-money $100 strike AAPL put option contract for $5.00 with a delta of -0.5 and the price of AAPL increases to $101, all else equal, the price of the contract would decrease to $4.50

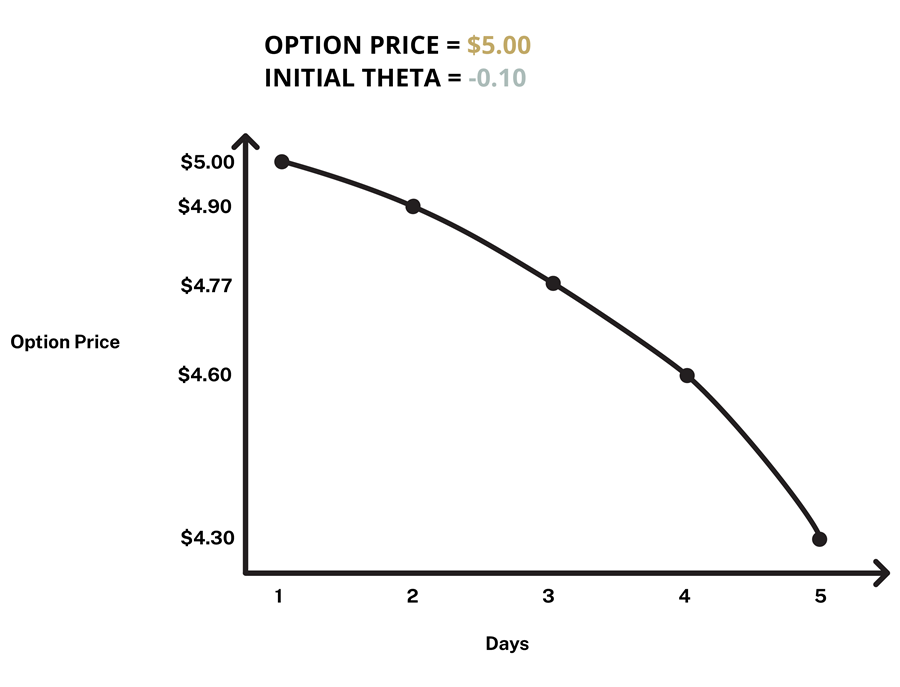
Theta

Theta focuses on the time element of risk for option contracts. Since option contracts have expiration dates, theta tells you how sensitive the price of an option contract is relative to how much time is left for the contract and is often referred to as the “time decay” for the contract. Theta is typically negative when you purchase (are long) an option and positive when you sell (are short) an option. Theta exponentially increases if you are an option buyer and decreases for option sellers as the expiration date approaches, resulting in theta reading of 0 upon expiry.

Example #3 (Figure 3): If you purchased an at-the-money $100 strike AAPL call option contract for $5.00 with a theta of -0.10, all else equal, you would expect the contract to lose $0.10 of premium value after the first day of trading. As an option approaches its expiration date, theta “decay” will exponentially increase until the option has a theta value of 0.

Rho

Rho provides insight on interest rate risk pertaining to an option’s value by measuring the contract’s price sensitivity to a 1% change in the risk-free rate. Call options generally tend to benefit from interest rate increases while the opposite is true for put options.

Example #4: If you purchased an at-the-money $100 strike APPL call option contract for $5.00 with rho at 0.25 and the risk-free rate increases by 1%, all else equal, the contract value would increase to $5.25.

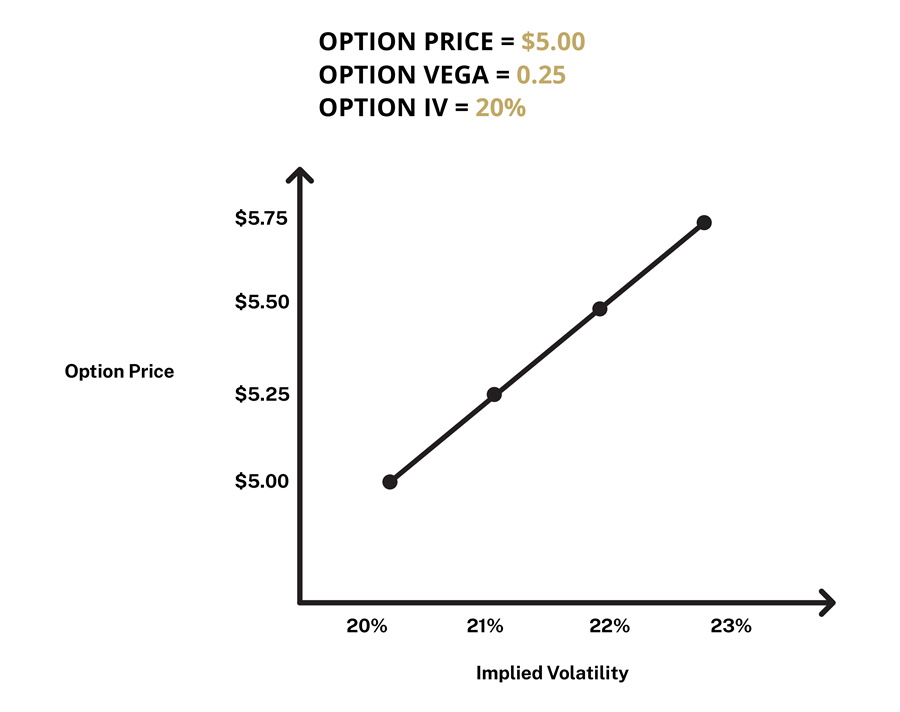
Vega

Vega measures the price sensitivity of an option contract to a 1% change in implied volatility. Increases in implied volatility (IV) generally result in an increase in the value of the option contract, whereas decreases in IV generally result in a decrease in value, all else equal.

Example #5 (Figure 4): If you purchased an at-the-money $100 strike AAPL call option contract for $5.00 with vega at 0.25 and an initial IV of 20%, and IV increases to 21%, all else equal, the price of the contract would increase to $5.25.

Second-order Greeks

Gamma

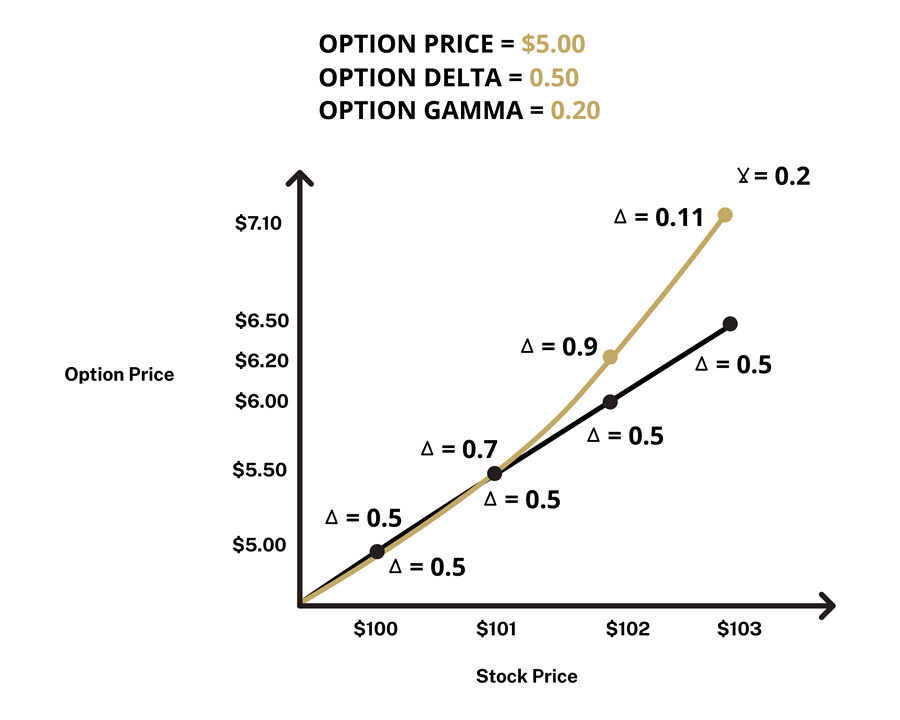
Gamma is a second derivative option Greek that measures the sensitivity of the rate of change of the option price (delta) for every $1 move in the underlying investment’s price. Long options have positive gamma and short options have negative gamma. Long options generally have a positive relationship with gamma as the option moves further in the money, while the inverse is true for short options. Gamma values are generally smaller the further away from the date of expiration as options with longer expirations are less sensitive to delta changes. Changes in gamma can produce positiveconvexity as deep out-of-the-money options move closer to moneyness.

Example #6 (Figure 5): If you purchased an at-the-money $100 strike AAPL call option contract for $5.00 with a delta of 0.50 and a gamma of 0.20, and AAPL increases by $1, all else equal, the delta would increase by 0.20. The figure below shows that when the price of AAPL increased from $100 to $101, the respective option price increased by $0.50. An additional stock price increase to $102 or higher would impact the option contract’s gamma by 0.20 per dollar gained on the stock price, resulting in an increase of the option’s delta and responsive option price.